@Psyhbf 你的理解是对的。

“从整个动作集中选”指的不是说迭代的时候使用的策略，迭代时策略的动作是什么就按照什么去选择。

“从整个动作集中选”指的是在策略提升时，求argmax时，会从整个动作集中求argmax，即要比较argmax_a Q(s, a)。

同学你好：

你产生奇异矩阵的原因是因为你的状态转移矩阵有一些问题。

你的转移矩阵第一行是[1, 0, 0, 0, 0]，说明这个状态会无限跳转到自己本身。这是一个终止状态？终止状态的话，是直接定义的，不需要求解。

@twxjyg 出现这种情况，一般是因为下面两个条件同时发生，1. 在你的策略下会有环状的状态转移持续进行。比如在课件中的例子，你的策略是一直“玩手机”。2. 你设置了gamma=1。在这样的情况下，玩手机的值函数会变成无穷大（正无穷大或者负无穷大）

这种情况是不能通过矩阵的方法求出来的

可以解啊，利用矩阵的形式直接可以直接求啊。

引用回答

http://www.shenlanxueyuan.com/course/107/thread/160

同学你好：

是指每个状态的值函数都要好于另一个策略的值函数

同学你好，

想问一下，这是哪一次的作业呢？

这里没有写终止状态，因为终止状态的值函数是已知的，所以不需要求。另外一方面，对于agent来说，终止状态时不需要做出决策。

同学你好：

这个是由状态转移矩阵决定的。很多情况下，状态转移都是不确定的。比如你跟别人下围棋，我们把对方视为环境，当你下了一个棋子之后，对方给的反馈就是随机的。你只能估计对方在某个地方落子的概率，而无法得到准确的值。

同学你好：

值函数是客观存在的，策略迭代和值迭代都是为了找到这个客观的值函数。所以应该是相同的

同学你好：

抱歉之前没看到你的完整代码，你现在的代码应该是正确的。

准确点说，这是根据链式法则导出来的。

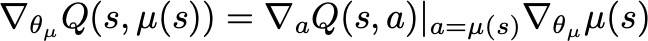
因此直接这样算即可。需要注意的是，这里在求actor loss的时候，注意不要使用样本中的action，而要使用mu的输出。

同学你好：

这个问题属于强化学习中的动态规划中的重要问题。我这里一两句的话也讲不清楚，而且我们的课程在第三章讲到动态规划时，会对其进行详述。因此，如果你不是特别着急的话，我相信你会在第三章获得详细的了解。

我的印象中好像是这篇文献，你可以考虑查一下。

GPOMDP: BartleB &Baxter, JAIR 2001

同学你好：

本质上都是做一样的事，都是想求出Q，但是一个是通过了采样去拟合，另一个是通过求出模型之后，用模型来求。都是一样的事，但是求的方法不同而已。

@hth945 你说的很有道理。虽然不同的方法目的是一样，但是不同的方法总能达到不同的效果。通过采样一些样本学习出来一个环境模型，是能够通过这个环境模型生成大量的样本的。

同学你好：

这道题我理解主要是将公式(6.5)替换成更新公式。公式6.5描述的是V(St+1)和V(St)的关系，但是真正的更新公式是和步长相关的。你这个证明，我看了下，应该思路没啥问题，可能需要检查下下标啥的（你拍的下标我没怎么看清）

同学你好：

函数近似的时候，就不存在更新的时候不相互干扰。本身动作空间就是连续的，而且也是无限维度的，因此如果更新动作的时候都是独立的话，那么就永远会存在一些动作不会被更新到。函数近似的一个优点就是更新动作a的时候，动作b也会受到影响，假设所有的动作之间存在某种规律，那么我按照代表的几个动作更新，就能拓展到所有的动作。

同学你好：

第一个问题：你看一下最优值函数差的多不多？如果差很多的话，有可能是采样不够。

第二个问题：1， 一条轨迹是可以进行多次策略评价的。因为一条轨迹可以构造出很多子轨迹。

2，策略提升的间隔可以自己随意设置，间隔越大，更新越稳定，但是越慢。间隔越小，更新越快，越震荡。

@陈皖玉 第四章的算法是基于值函数的方法，是否收敛主要判断的是值函数，如果值函数稳定下来才算收敛。第二点，你这种情况，有可能是探索不够。在探索不够的情况下，很容易自我收敛。

同学你好：

其实并不矛盾，我们做公式推导时考虑的是一条轨迹的过程。但是实际操作的时候是单步更新。实际上每一条实际的轨迹是可以拆分成很多条子轨迹的，单步更新指的就是子轨迹下更新。