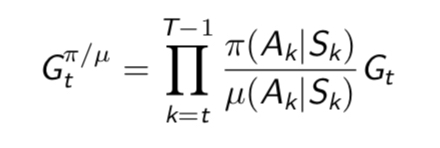-
同学你好:
这里的k表示迭代步数。用之前第k步的值函数更新第k+1步的值函数
-
关于第四节作业一些疑问
——来自《强化学习理论与实践- 第一期》·60浏览
同学你好:
你要结合MC的问题去思考,MC本质上是利用了统计平均值去估计真实期望值.
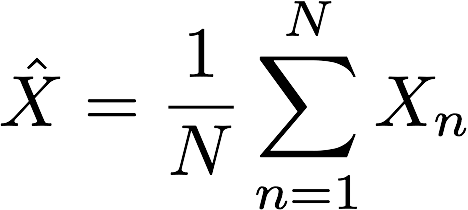
每个Xn代表回报值。回报值是一个随机变量,我们用Xn的平均值来估计Xn的真实期望值。
每做一次实验,得到的Xn都是独立同分布的,假设Xn是均值为u, 方差为q的随机变量。
这个作业的目的是,让你求
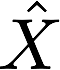 的方差和N之间的关系
的方差和N之间的关系 -
关于第四节作业一些疑问
——来自《强化学习理论与实践- 第一期》·60浏览
@linjianbing 其实这个解答很简单,主要考察的是大家能不能把平时学到的知识用起来。同学你可能想得复杂了
因为Xn都是来自均值为u,方差为q的分布,且相互独立。
所以
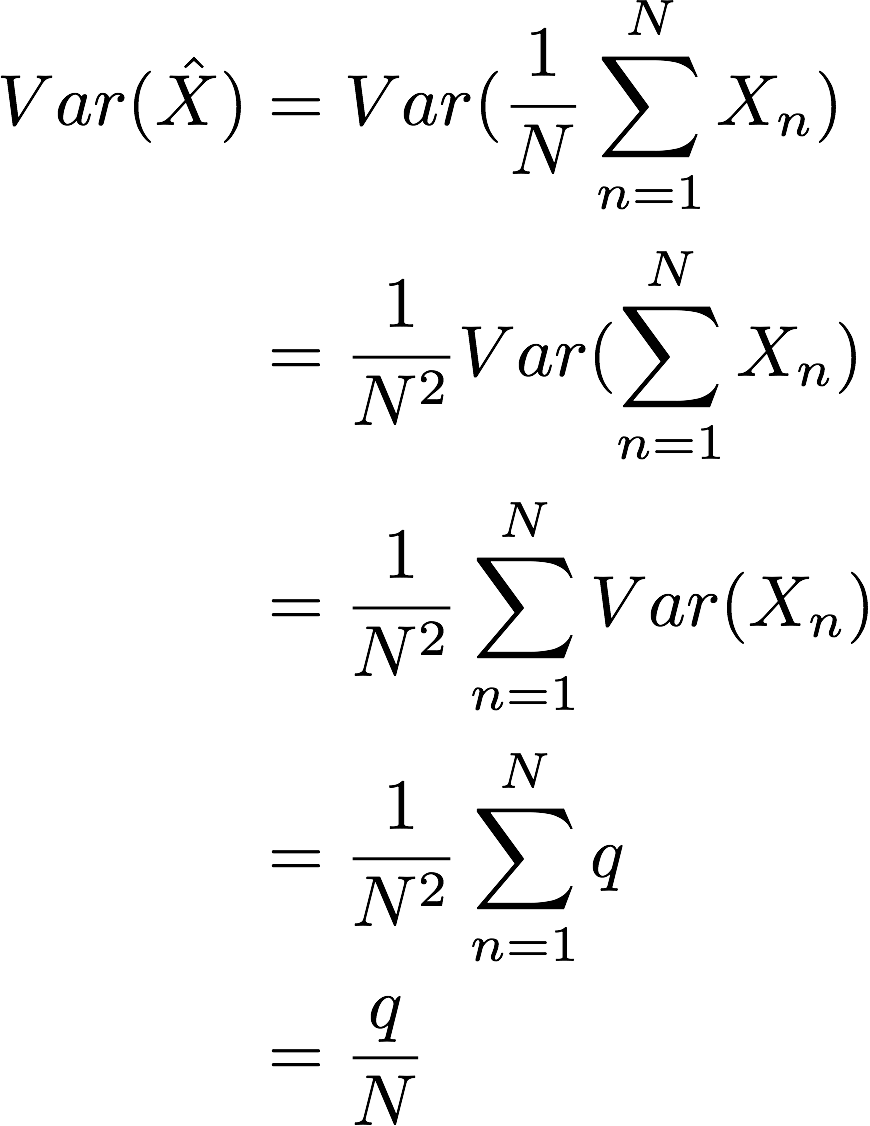
其中第三个等号,利用了每次采样都是独立的。这样就可以得到MC估计的方差随着N的增大,成反比例减少的关系了
-
同学你好:
神经网络一个著名的特点就是局部最优,扰动之后,不能保证收敛到原来的值。
-
关于前向视角和后向视角下的误差等价公式推导的疑问
——来自《强化学习理论与实践- 第一期》·11浏览
同学你好:
最后一项是终止状态,终止状态的值函数我们一般是预定义好的,比如等于0
-
TD(λ)的前向视角为什么只能从完整的片段学习?
——来自《强化学习理论与实践- 第一期》·19浏览
同学你好:
1. TD(lambda)和n步TD是不同的哈。n步TD看n步就行了,TD(lambda)中包含了MC项,所以必须要完整片段。
2. 在线更新指一遍跟环境交互,一遍更新。有时候不一定是每步的,比如每2步,每3步等。
-
关于资格迹的问题
——来自《强化学习理论与实践- 第一期》·10浏览
同学你好:
因为那个是“终止状态”的值函数,一般定义为0
-
第五章TD作业1中的BUG问题
——来自《强化学习理论与实践- 第一期》·35浏览
同学你好:
呃呃,应该是我在作业里忘记写一句话了:
我把V(右边停止状态)设为1的原因,是为了简化大家的计算,因为V(右边停止状态)= 1的话,我们可以把所有的r都看成0。这是一个trick。作业里没这么写,确实容易引起误解,抱歉哈。
-
关于蒙特卡罗优化算法每次访问的问题
——来自《强化学习理论与实践- 第一期》·16浏览
同学你好:
每次遇到动作对<s,a>就+1。它本质上是统计<s, a>出现过多少次
-
同学你好:
并不是说Q和策略没关系了。Q和策略是有关系的。按照Q的定义,在状态S下做动作A,然后再按照策略π获得的期望回报值。因此Q的值跟策略是相关的。
那为什么这里Q学习的重要性采样率和策略无关了呢?
原因在于TD算法中,我们学习Q时,只采样了单步的S和A。而根据Q的定义,Q跟策略的关系是存在于做完A之后。而重要性采样率是作用在采样S和A的时候。因此这里的重要性采样率和策略无关。
并不是学习Q函数就不要重要性采样,比如利用MC学习Q函数是需要重要性采样的。
另外:“Q学习”是一个专有算法,并不是指学习Q函数的意思,它特指利用TD(0)算法,求解最优Q函数的算法。
-
关于第四讲课后编程题,采样轨迹的终止条件
——来自《强化学习理论与实践- 第一期》·49浏览
同学你好:
你这个问题提的很好。确实是我疏忽大意。当时设计这个作业,主要是有两方面的考虑:
1. 重复利用上节课的环境,减少环境的编程量。
2. 可以与动态规划的算法作为一个比较。
有一种MC方法是可以不用完整轨迹的。但是这种方法在第6章,讲资格迹的时候才会提及,而且也不是本节课的要求。因此这里确实是我欠考虑了。
不过,停止条件有很多设置的方法,当衰减系数小于1时,可以设置一定的步数之后,自动结束片段。因为衰减系数的作用是指数形式,等一定的步数之后,对值函数的贡献是可以忽略不计的了。比如这里可以设置T=30
-
关于第四讲课后编程题,采样轨迹的终止条件
——来自《强化学习理论与实践- 第一期》·49浏览
这里的gamma
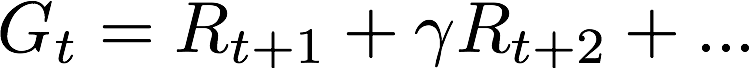
-
epsilon-greedy编程
——来自《强化学习理论与实践- 第一期》·20浏览
同学:
主要原因是,有可能有几个动作都能导致最大的Q值。比如Q(s, a1) = 0, Q(s, a2)= 1, Q(s, a3) = 1, 这里a2, a3都能导致最大的Q值,这句话的意思就是会在a2,a3中随机选择
-
epsilon-greedy编程
——来自《强化学习理论与实践- 第一期》·20浏览
@橘朵 同学你好,这个是python中独有的列表生成式,专门用来构造列表,是一种效率较高的简易写法。
即:
a = []
for action_, value_ in enumerate(values):
if value_ == np.max(values):
a.append(value_)
currentAction = np.random.choice(a)
python中还有很多这种写法,除了构造列表外,还能构造字典等。
-
关于动态规划值迭代的问题
——来自《强化学习理论与实践- 第一期》·29浏览
同学你好:
很抱歉,我不是特别理解你说的是哪一幅图,能把你所说的图贴一下吗?也方面其他同学逛到这个问题时,能够直接理解你的问题,而不用去查阅ppt。
-
关于动态规划值迭代的问题
——来自《强化学习理论与实践- 第一期》·29浏览
@Albert 值迭代指的是利用上一次迭代的值函数,第二幅图迭代时是利用了第一幅图的值函数。因为第一幅图中的值函数都是0,所以第二幅图的结果基本都是-1,只有靠近重点的两个状态不同。
你所想的距离越远,值函数越小,是最终收敛后的结果,中间迭代过程并不是这样哦。
-
关于重要性采样与离策略MC策略评价的提问
——来自《强化学习理论与实践- 第一期》·35浏览
同学你好:
1. 我们定义轨迹S1, A1, S2, A2,...,每条轨迹出现的概率会随着策略的不同而不同。在强化学习中,我们评价的策略是π,但是真正去采样的策略是u,因此重要性采样率就是策略为u的情况下轨迹出现的概率和策略为π下,轨迹出现的概率的比值
2. π并不是无法直接采样的,而是因为很多时候为了更多的探索,我们需要使用另一个策略去采样。比如,当我们想要得到一个确定性最优策略π时,如果直接用π去采样,会导致每个状态s下都会对应到唯一的动作a,而我们需要考察一下其他的a好不好,因此会使用一个探索性更强的策略去采样
3. 从后往前计算,是为了减少计算量。比如轨迹S1, A1, S2, A2, S3, ....,我们可以先算出S3处的回报值G3,用G3可以更新S3的值函数。然后计算G2时,可以利用G2=R3+yG3。如果从前往后算,复杂度会高些
-
关于重要性采样与离策略MC策略评价的提问
——来自《强化学习理论与实践- 第一期》·35浏览
-
关于最优值函数与最优Q函数问题
——来自《强化学习理论与实践- 第一期》·26浏览
同学你好:
1. 最优Q函数也是最优值函数的一种,最优值函数就包括了最优V函数和最优Q函数
2. 最优策略可能有很多,所以永远不能说明最优策略相同。比如如果Q(s,a1) = Q(s, a2) = max Q(s, .) , 即最优策略有可能选a1,也有可能选a2
3. 最优V函数和最优Q函数都是唯一的,也就是说最优值函数和最优策略是一对多的关系
-
关于最优值函数与最优Q函数问题
——来自《强化学习理论与实践- 第一期》·26浏览
@linjianbing 最优V函数和最优Q函数是一一对应的,参考贝尔曼最优方程,两者之间有着唯一确定的关系。