同学你好：

1. 根据v函数的定义，它表示在状态s下，根据策略pi，所获得的期望回报值，而策略pi是描述的是动作的分布。而Q函数的定义在在状态s下，做动作a，然后按照策略pi所获得的期望回报值。这中间就差了一个动作a是怎么选择的？根据v函数的定义，它表示a是服从策略pi的分布的，因此使用pi对Q进行加权求和就能得到期望值，即v函数

2. 第二个图和第一个图的含义相同，但是由于最优的策略具备一个性质，它表示选择了Q值最大的动作，因此求期望就相当于求max

3. 第三个图就是通过贝尔曼最优方程将Q*与V*的关系，以V*与Q*的关系组合起来即可得到。 

@勇往直前zyw 

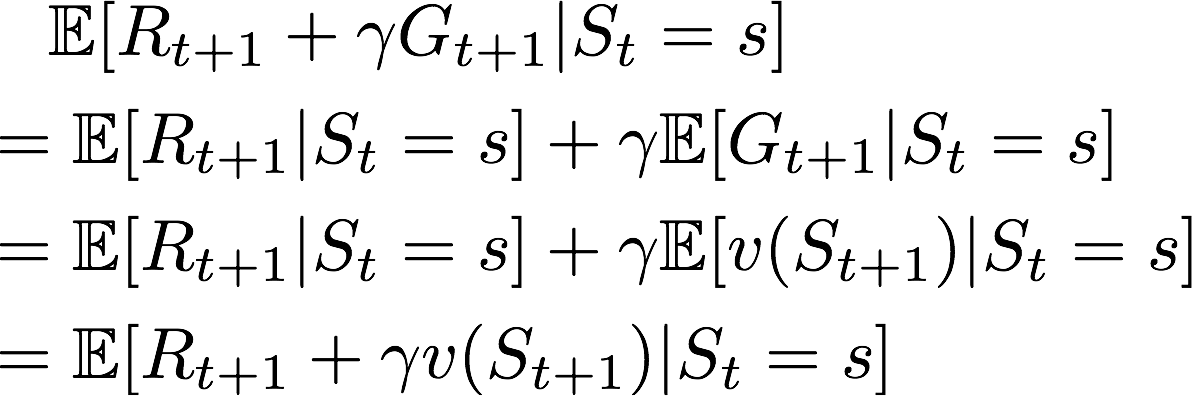
同学你这个定义不太对哦。v函数的定义应该是针对小写的s的，大写的S是随机变量。

所以v(S_{t+1}) 是一个随机变量，对其求期望，即对S_{t+1}的分布加权求和。

G_{t+1}也是一个随机变量，在已知S_t的情况下，G_{t+1}求期望是需要对两个分布加权求和的，一个是S_{t+1}的分布，另一个是在给定S_{t+1}的情况下，G_{t+1}的分布。

但是无论如何，两者在期望的情况下，都是相等的。总而言之，在有期望符号的情况下，回报值是等价于值函数的。

同学你好：

在这里初始状态影响不大，因为所有的环境转移都是已知的

确定性策略是表示我在状态s下，会一定选择动作a，而不是随机采样一个动作a

我举只有两个状态，两个动作的例子：（图中的数字表示执行某个动作的概率），左边就是一个确定性策略，右边就是一个随机策略

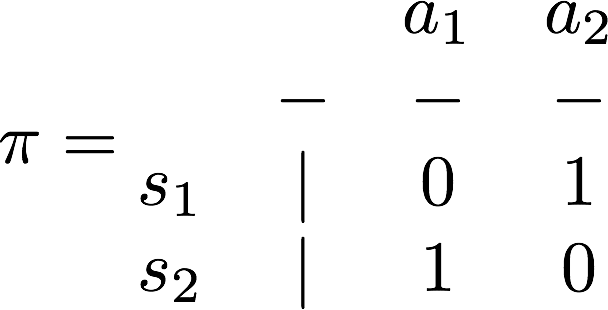
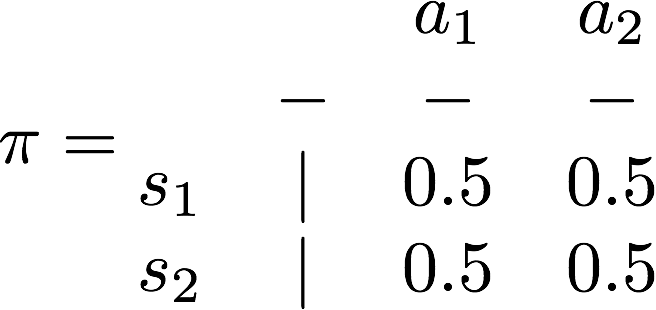
作业中，我举一个确定性策略的例子，如下。由于每个s处，只能选两个动作，所以即使穷举也只有16种

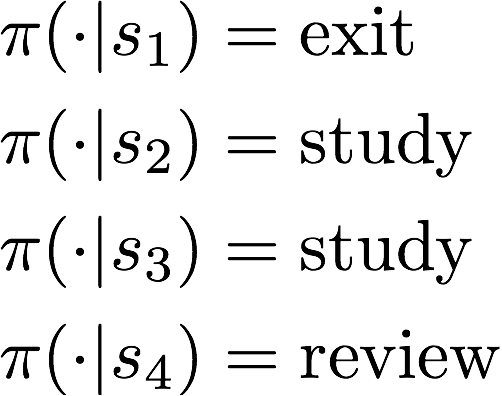
同学你好：

你这样理解是不对的。

P跟π是不同的，MDP中的P指的是在状态s下，做了动作a，跳转到s'的概率。

π指的是在状态s下选择动作a的概率

如果在状态s，做了动作a，能够确定跳转到某个固定的状态s'，那么确实如你所说，动作影响了状态转移

但是会存在在状态s下做了动作a之后，不确定跳转到哪里，这个就是MDP中的P所描述的。准确的说，MDP中的P是一个三维矩阵，即P(s, a, s')。

在我的ppt的37页，你可以看在“科目三”处，选择“不复习”这个动作，最终的后继状态仍然是随机的，这个随机性是在P中描述，π只描述了是否选择“不复习”这个动作

同学你好：

抱歉我不太理解你的多个episode的任务是什么，能举例说明吗？

同学你好：

你说的这个问题，只是一种定义上的习惯，也存在有一些地方会使用角标t，即把奖励获得和状态看成同一个时刻的。

不过大部分问题都会认为奖励的获得是来自下一个时刻，主要原因是环境的反应时间。假设智能体的是可以瞬间作出决策，那么智能体根据St作出决策At，环境可能需要一定的反应时间，才能返回奖励R和下一个状态S_{t+1}, 因为奖励总是和下一状态一起到来的，所以一般来说就把它的下标设置为t+1了。

在这里的马尔可夫奖励过程中，设置成t+1是沿用了马尔可夫决策过程中的定义。

同学你好：

假设一条马尔可夫链为s1, a1, s2, a2, s3, a3 ......

q(s, a)表示初始状态和初始动作确定了s=s1, a=a1，之后的动作a2, a3，...都是来自策略π 的

所以与你说的并不矛盾啊。

而且，观察你后面所写的公式中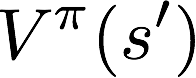也是表示从s'开始执行策略π。

@luweikxy 对的

同学你好：

如果知道v*之后，我们在每个状态的最优动作，即

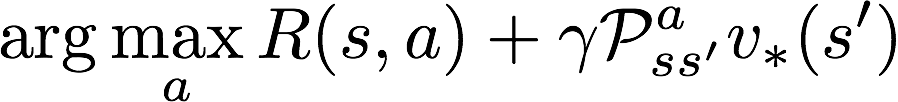
观察哪个动作可以让R+yPv*(s')最大即可

参考ppt的48页，可以通过最优Q函数直接得到最优策略。只是这个时候得到最优策略是确定性策略，即它的概率分布是在某个动作上的概率为1，其他的动作概率为0

同学你好：

这里的状态值函数是通过解贝尔曼方程求出来的。通过定义是没法直接求出值函数的

同学你好：

1. 奖励求期望，是因为奖励有可能是随机值。比如课堂上的例子，我定义通过考试为+10，但是有些时候可以将奖励定义成考试的分数，这个时候能获得多少奖励，就是随机的。你只能说你学得好，大概可以考90分，但是与出卷难度是息息相关的。在MRP中，如果到达状态s，获得奖励是确定的，那么期望符号就可以去掉，如果是随机的，我们关注的是它的期望值。

2，求期望主要有两种办法，一种是如果已知概率分布，那么可以用概率分布求和的方式。另外一种是通过采集样本，然后用样本均值估计总体期望。在MRP和MDP中，直接解贝尔曼期望方程本质是就是利用了概率分布P和pi。后面的课程也会讲述其他的求解方式。

同学你好：

1. 根据值函数的定义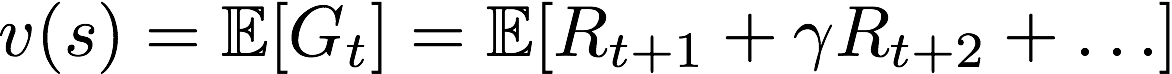：，终止状态后的R_{t+1}都为0（参考我ppt中片段性任务和连续性任务的统一表达），因此终止状态的值函数定义为0

2. 一般来说，良好定义的MRP都是有唯一解的。原因在于a, 首先每个状态都能写出一个贝尔曼期望等式，所以(I-yP)是一个方阵；b, 良好定义的每个贝尔曼期望等式都是具备信息量的（也就是不能被其他贝尔曼等式所线性表达），所以是一个满秩矩阵，因此可以求逆。

如果没有唯一解，代表存在非正常状态，该状态的贝尔曼期望等式不包含信息量。这种状态意味着重复定义了，需要从状态集的定义中删除。

这个问题，我过去没有仔细思考过，所以一时不能给出完全公式化的表达。如果我哪天想到了，会补充该答案

3. 在MDP中，如果求出的最优V，可以通过贝尔曼最优方程得到最优Q。参考ppt 51页。

同学你好，据我所知，minimax的问题会假设对方是在一个最优的情况，它解决的是在对方在最大化胜利概率的情况下，己方该怎么做的问题。minimax的方法，会尽可能下的好，都会按最优的方法去做，不会去到达一个可能会输的状态。强化学习不一样，通过学习后，发现对方喜欢犯错，会利用对面犯错，然后赢得比赛。

本书中的意思是：如果按照minimax，后手下是不可能赢的，对方如果是完美的棋手，后手最多打平。如果是强化学习，后手是有赢的概率的，因为对方会犯错。可以学习到如何利用对方犯错。

同学你好，公式中的I是指单位矩阵，而不是数字1。可能没有写特别清楚。。。

我知道你的问题在哪里了。你应该不考虑终止状态的，本质上的问题是“通过考试”百分百会跳转到终止状态，这两者在P中的表现完全一样，即两者所对应的p向量可以相互线性表达。

而且由于终止状态的值函数就是0，不是这里的未知数。

同学你好。

1. 强化学习是根据当前状态做出决策的。只是当前状态的定义有很多种，一种是定义为历史所有数据。但是总归是可以观察到当前状态的。

2. 动态系统的决策算法本身就可以用强化学习算法去解。一般来说强化学习是解决动态系统的手段之一。是否观察到当前状态与是不是强化学习算法没有直接的关系。

3. 凸优化只是强化学习的一种工具，并不是算法的本质。其他学习算法也可以使用凸优化技术。

抱歉同学，没能完全理解你的问题。不过你如果有疑惑，后面的课程会对强化学习有更加深入的讲解，或许能对你的问题有所帮助。

@hehuaiwen 原来是在线学习技术，我对online的学习算法了解比较浅陋，感谢同学的指出，学习了！

同学你好，环境模型指的是状态转移函数和奖励函数。只要知道函数关系即叫做知道环境模型了。

知道环境模型和全观测是两个不同的概念。

全观测指的是智能体能看见所有环境的相关信息。环境模型指的是我能预测我在某个状态下做了动作会跳转到哪一个新状态，并获得多少奖励。

一般来说，已知环境模型的假设更强，因为这意味着不仅仅能观测到环境，还意味着掌握了环境的动态特性。

举个下围棋的例子，如果定义当前棋盘为状态，那么因为可以看见完整对局，所以是全观测的。但是由于不清楚对手下一步该怎么下，因此无法预测棋局的变化，因此属于未知环境模型。